Great How To Draw An Asymptote in 2023 Learn more here

Ck12 foundation

Table of Contents

If you’ve ever wondered how to draw an asymptote, you’re not alone! Many people struggle with this topic, but it’s actually not as difficult as it may seem at first glance. With a little bit of knowledge and practice, anyone can learn how to draw an asymptote with ease.

Pain Points

Have you ever found yourself struggling to graph a function because you couldn’t identify the asymptotes? Or maybe you’ve spent hours trying to figure out how to draw an asymptote correctly, but always ended up with a graph that looked wrong. These are common pain points that people face when dealing with asymptotes.

Target: How to Draw an Asymptote

To draw an asymptote, you first need to understand what it is. An asymptote is a line that a function approaches but never touches. There are three types of asymptotes: horizontal, vertical, and slant. Horizontal asymptotes occur when the function approaches a specific y-value as x approaches positive or negative infinity. Vertical asymptotes occur when the function approaches infinity or negative infinity as x approaches a specific value. Slant asymptotes occur when the function approaches a line as x approaches infinity or negative infinity.

Main Points

To draw an asymptote, you need to understand the three types of asymptotes: horizontal, vertical, and slant. You also need to know when each type of asymptote occurs and how to identify it on a graph. With this knowledge, you can easily draw asymptotes for any function you encounter.

Horizontal Asymptotes

One way to identify horizontal asymptotes is to look at the degree of the numerator and denominator of the function. If the degree of the numerator is less than the degree of the denominator, then the horizontal asymptote is y = 0. If the degree of the numerator is equal to the degree of the denominator, then the horizontal asymptote is the ratio of the leading coefficients. If the degree of the numerator is greater than the degree of the denominator, then there is no horizontal asymptote.

Vertical Asymptotes

To find vertical asymptotes, set the denominator of the function equal to zero and solve. The resulting values of x are the locations of the vertical asymptotes. If the numerator is also equal to zero at the same x-value as the denominator, then the vertical asymptote is a removable singularity. Otherwise, the function approaches infinity or negative infinity as x approaches the vertical asymptote.

### Slant Asymptotes

Slant asymptotes occur when the degree of the numerator is exactly one greater than the degree of the denominator. To find the equation of the slant asymptote, divide the numerator by the denominator using long division. The quotient is the equation of the slant asymptote, which is a linear function. The remainder is a fraction with a denominator equal to the denominator of the original function. This fraction approaches zero as x approaches infinity or negative infinity.

Personal Experience

When I first started learning about asymptotes, I found it difficult to understand how they could exist without touching the function. However, after I learned more about the different types of asymptotes and how to identify them, I was able to graph functions much more accurately.

FAQ

How do you know if a function has an asymptote?

A function may have an asymptote if it approaches infinity or negative infinity or approaches a specific value as x approaches infinity or negative infinity.

What is the difference between a horizontal and vertical asymptote?

A horizontal asymptote occurs when the function approaches a specific y-value as x approaches positive or negative infinity, while a vertical asymptote occurs when the function approaches infinity or negative infinity as x approaches a specific value.

Can a function have more than one asymptote?

Yes, a function can have multiple asymptotes of different types.

Do all functions have asymptotes?

No, not all functions have asymptotes. Only functions that approach infinity or negative infinity or approach a specific value as x approaches infinity or negative infinity have asymptotes.

Conclusion of How to Draw an Asymptote

Drawing an asymptote doesn’t have to be difficult. By understanding the types of asymptotes and how to identify them, anyone can draw an asymptote for any function. With practice, this process will become second nature, and you’ll be able to graph functions with ease.

Gallery

CK12-Foundation

_{^{Photo Credit by: bing.com /}}

5.6 Sketching Graphs Of Functions

_{^{Photo Credit by: bing.com / asymptote graph oblique sketching graphs fig}}

Tikz Pgf - Asymptotes In A Plot - TeX - LaTeX Stack Exchange

_{^{Photo Credit by: bing.com / plot asymptote asymptotes vertical example asy modification slight why stack}}

Math Scene - Functions 2 - Lesson 3 - Rational Functions And Asymptotes

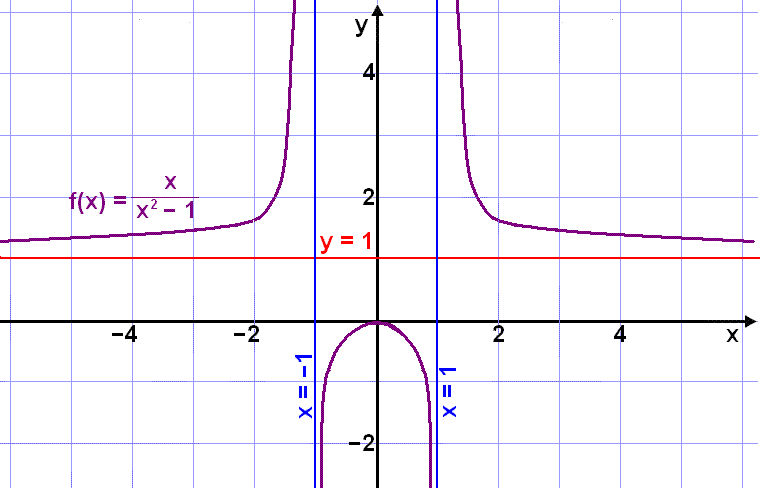
_{^{Photo Credit by: bing.com / graph functions rational equations math asymptotes equation google diagram vertical horizontal function find lesson line gr solve gif solving graphing}}

Asymptotes | Horizontal, Vertical Asymptotes And Solved Examples

_{^{Photo Credit by: bing.com / asymptotes asymptote curve horizontal approaches line moves infinity towards but vertical}}