Derivative graphing slope curve calculus inference differentiation
Table of Contents
Table of Contents
If you’re studying calculus or advanced math, you might have come across the problem of drawing a derivative graph from an original graph. This can be a daunting task for many, and it requires a deep understanding of the concept of derivatives. In this article, we will explore how to draw derivative graph from original graph, and provide you with some tips and tricks to make it easier.
Many students struggle with drawing derivatives because they don’t fully understand the concept. They know that a derivative is a line that represents the slope of a curve, but they don’t know how to translate that into a graph. This can lead to frustration and confusion, which can make studying calculus feel overwhelming.
The key to understanding how to draw derivative graph from original graph is to first understand the relationship between the two graphs. The derivative graph is essentially the “slope” of the original graph. To find the derivative graph, you need to find the slope of the original graph at each point, and plot those values as points on a new graph. This can be done manually, or with the help of software.
So, to draw a derivative graph from an original graph, you need to find the slope of the original graph at each point. This can be done by calculating the derivative of the original function at each point, or by estimating the slope using tangent lines. Once you have the slope values, you can plot them as points on a new graph. The resulting graph will be the derivative graph.
To summarize, we have explored how to draw derivative graph from original graph. We have discussed the pain points that many students face when trying to do this, and provided a solution to help make it easier. By understanding the relationship between the two graphs and finding the slope at each point, you can create an accurate derivative graph.
How to Draw Derivative Graph from Original Graph: Tips and Tricks
When I was first learning how to draw derivative graph from original graph, I found it helpful to break the process down into smaller steps. Here are some tips and tricks that I found useful:
1. Start by understanding the concept of derivatives. Make sure you understand what a derivative is and what it represents.
2. Plot the original graph on a coordinate plane.

3. Estimate the slope of the graph at each point, either by hand or with the help of software.

4. Plot the slope values as points on a new graph.
Understanding the Relationship Between the Two Graphs
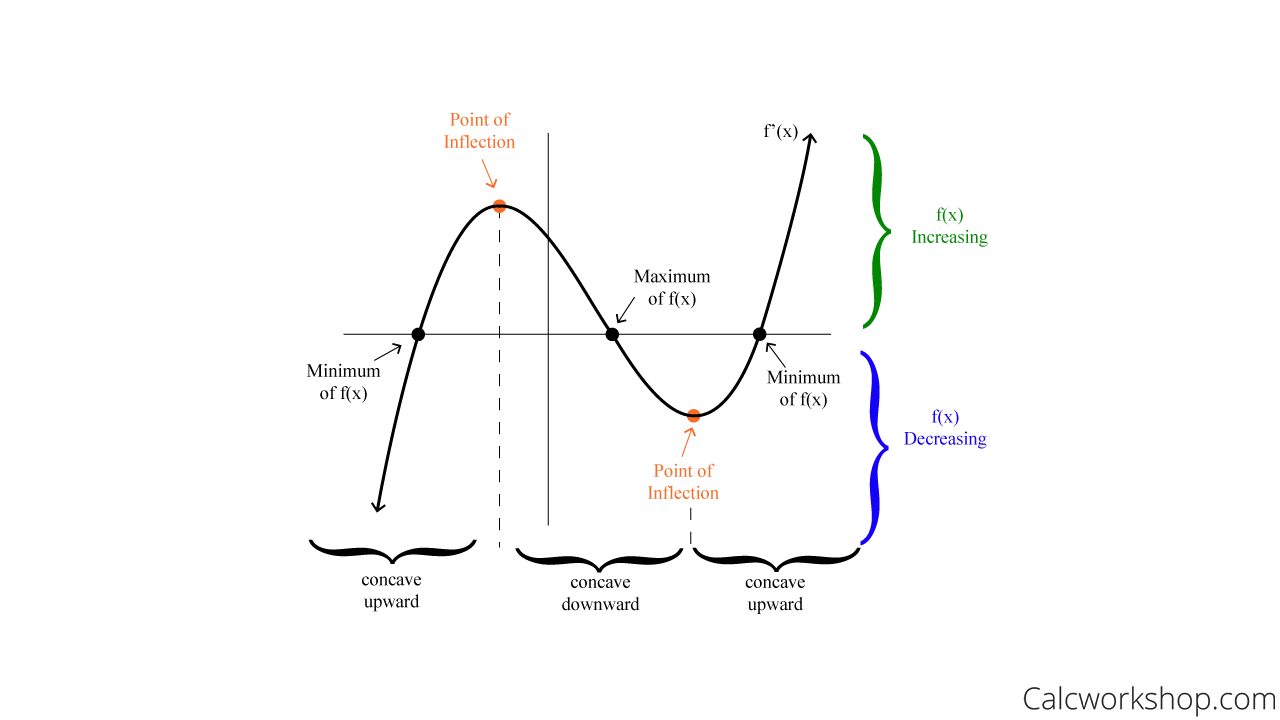
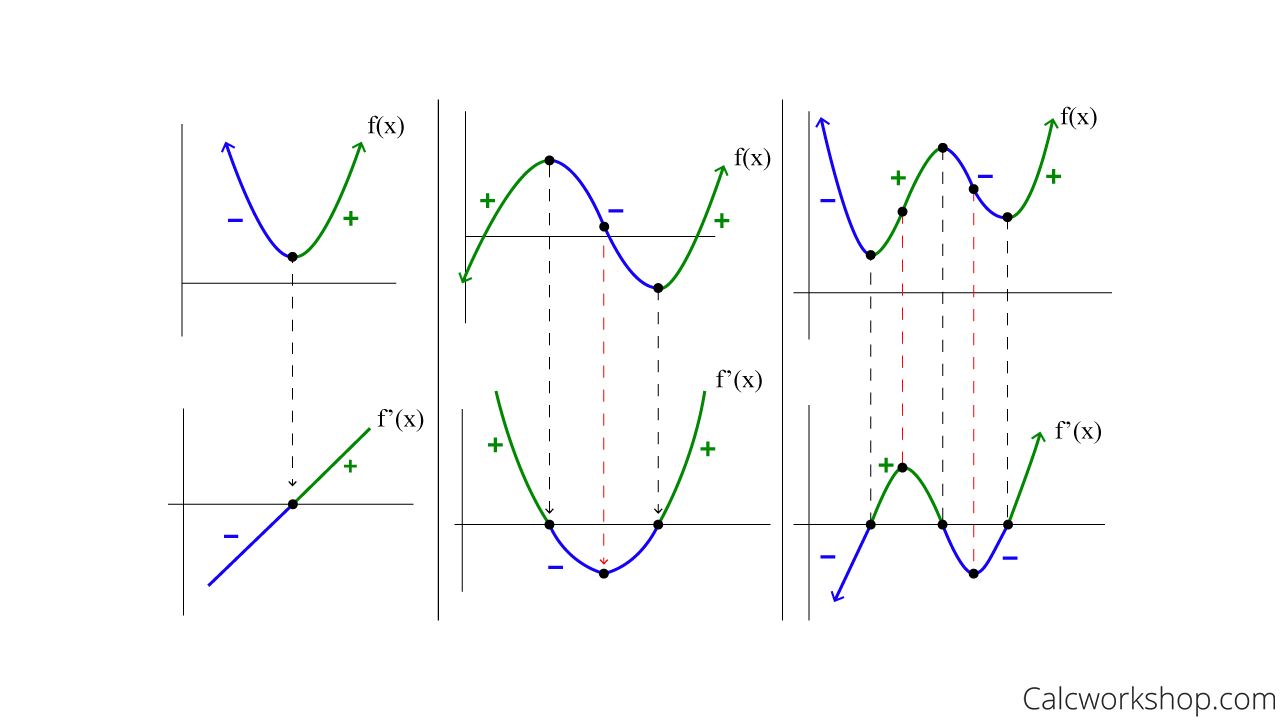
The key to drawing derivative graph from original graph is to understand the relationship between the two graphs. The derivative graph represents the slope of the original graph at each point. This means that if the original graph is steep, the derivative graph will have a high slope value. Conversely, if the original graph is flat, the derivative graph will have a low slope value.
One way to think about this is to imagine driving a car along the original graph. The derivative graph would represent the car’s speedometer. If the car is driving uphill, the speedometer will show a high speed. If the car is driving on a level road, the speedometer will show a moderate speed. And if the car is driving downhill, the speedometer will show a low speed.
Tips for Estimating Slope
Estimating the slope of the original graph can be a bit tricky, especially if the graph is complex. Here are some tips to help make it easier:
1. Use tangent lines. A tangent line is a straight line that touches the graph at a single point. By drawing tangent lines at different points along the graph, you can estimate the slope at those points.

2. Increase your accuracy by using software. While it’s important to understand how to estimate slope by hand, using software can help you get more accurate results. There are many graphing calculators and software programs available that can help you find the slope of the graph at each point.
Practice Makes Perfect
Learning how to draw derivative graph from original graph takes practice. Don’t be discouraged if you don’t get it right the first time. Keep practicing, and don’t be afraid to ask for help when you need it.
Question and Answer Section
Q: What is a derivative?
A: A derivative is a function that represents the slope of a curve at each point.
Q: Why is it important to understand how to draw derivative graph from original graph?
A: Drawing the derivative graph can help you understand the behavior of the original graph, and can be used to solve many real-world problems in fields such as physics, engineering, and economics.
Q: Can software be used to draw derivative graphs?
A: Yes, there are many graphing calculators and software programs available that can help you find the slope of the graph at each point.
Q: Can tangent lines be used to estimate slope?
A: Yes, tangent lines can be used to estimate the slope of the graph at each point.
Conclusion of How to Draw Derivative Graph from Original Graph
Learning how to draw derivative graph from original graph is an important skill for anyone studying calculus, physics, or engineering. By understanding the relationship between the two graphs and estimating the slope at each point, you can create an accurate derivative graph. Remember to practice, use software to increase accuracy, and don’t be afraid to ask for help when you need it.
Gallery
How To Draw A Graph Of A Function

Photo Credit by: bing.com / derivative
Draw The Function Given Graph Of Derivative - YouTube

Photo Credit by: bing.com / derivative graph function draw given
Find The Indicated Partial Derivative - Diehl Dalmor

Photo Credit by: bing.com /
Derivative As Slope Of A Curve Derivative And Direction Of A Function

Photo Credit by: bing.com / derivative graphing slope curve calculus inference differentiation
Derivative Graph Vs Original Function (w/ 15+ Examples!)

Photo Credit by: bing.com / derivative